My solution
1.
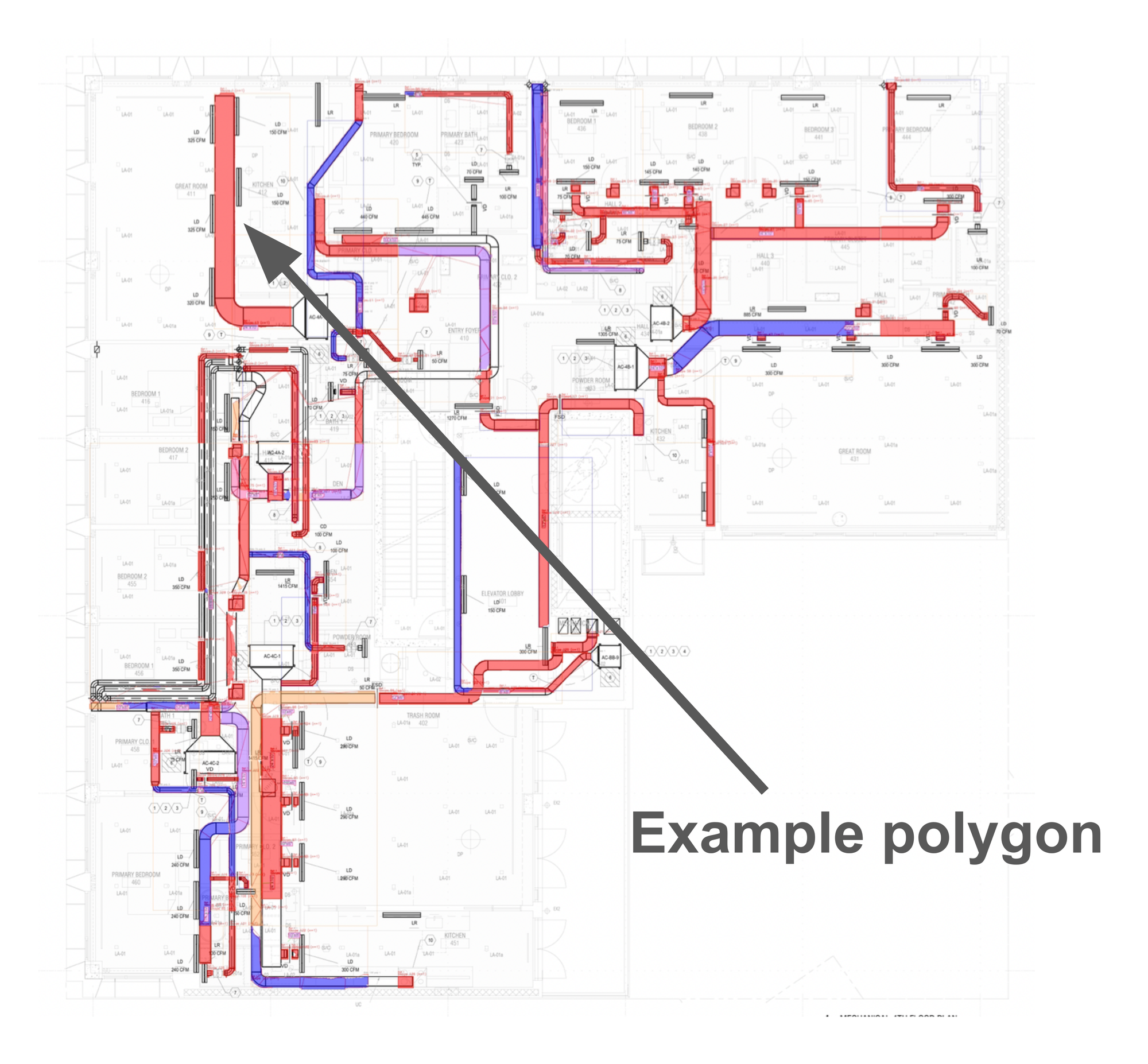
Read input_polygon1 as a list of vertices.
2.
Create a binary mask for the polygon.
3.
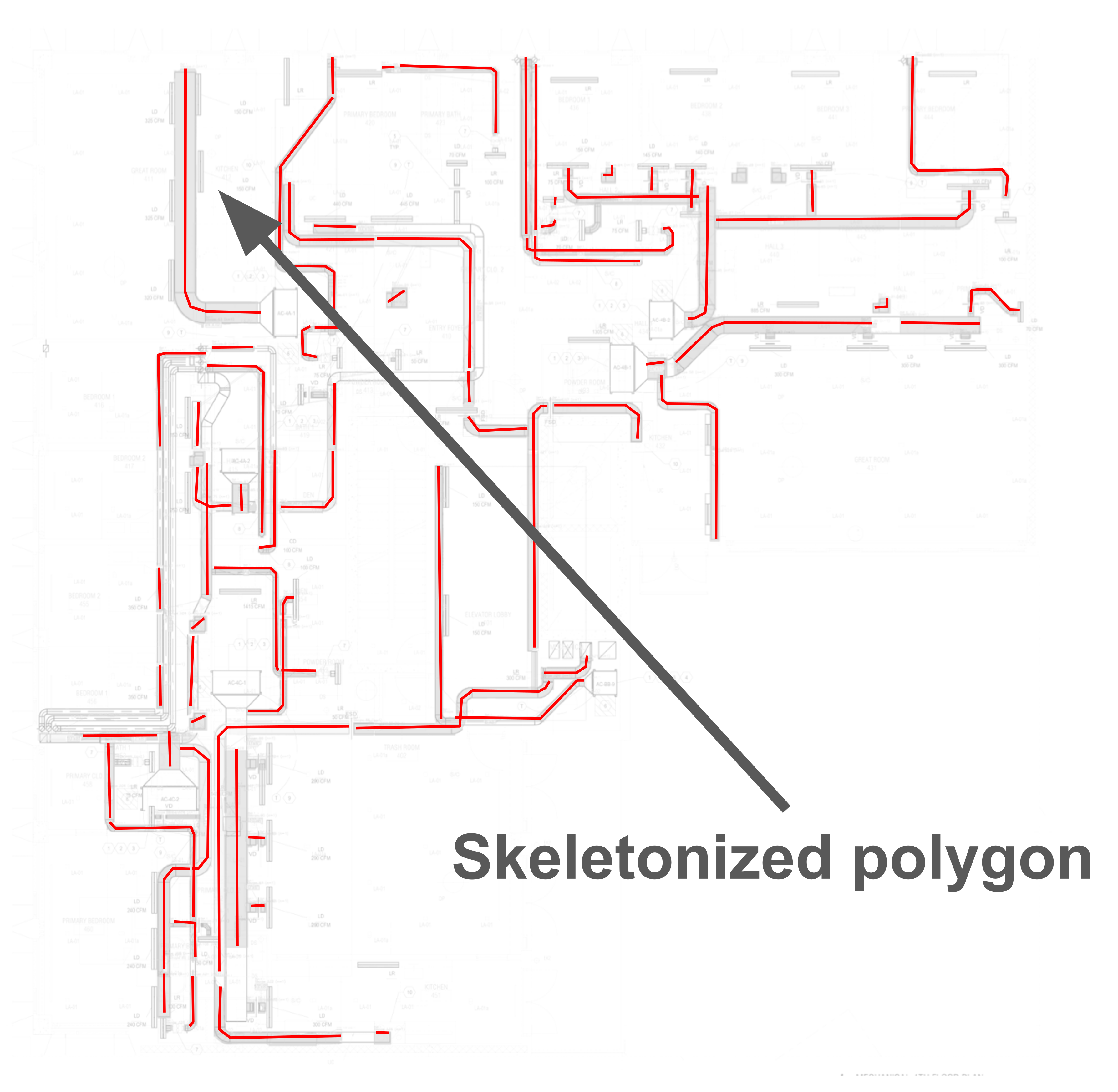
Call skeletonize of scikit-image to obtain a one pixel thick medial axis.
4.
Vectorize the skeleton.
For the algorithm «Skeleton Pruning by Contour Partitioning with Discrete Curve Evolution (DCE)» (Alg) from the article you linked (Article), it is necessary to be able to link the skeleton points with boundary points.
The vector model simplifies this logic.
To do this, it is necessary to represent the skeleton as a graph:
4.1.
Traverse the skeleton and link the pixels into a «edge-node» structure.
4.2.
For each branch (edge), attempt to determine «generating points» (the boundary points where this «maximal disk» tangentially touches the «planar set D» (the term from Section 3 of Article)) at least in those points that are nodes (bifurcation or endpoints).
Each skeleton point is the center of a «maximal disk» lying inside the figure and tangent to the boundary of the «planar set D».
«Generating points» are the boundary points where this «maximal disk» tangentially touches the «planar set D».
To determine «generating points»:
4.2.1.
For each skeleton point, find the «maximal disk» for which it is the center.
4.2.2.
Check the boundary segments where tangential contact might exist.
4.2.3.
Find the tangential points on the boundary segments.
4.2.4.
Exclude external or invalid intersections.
4.2.5.
Gather all such tangential points as the «generating points».
5.
Extract the polygon boundary.
5.1.
Prepare the contour.
We already have input_polygon1, which is a vector of vertices, and we must ensure that it is a complete contour, because Alg requires the boundary to be in polygonal form.
5.2.
Check for holes.
If the figure is not just one outer contour but also has inner contours (holes), we must provide each contour separately, as Alg requires.
6.
Call Alg and pass it:
6.1.
The boundary of the polygon, which is the list of vertices of the outer contour plus the list of vertices for each inner contour.
6.2.
The skeleton (in vector form).
6.3.
The desired simplification level.
6.4.
The parameter indicating at which step Alg should stop.
7.
Alg is implemented as follows:
7.1.
Simplify the boundary using the Discrete Curve Evolution (DCE) method.
7.1.1.
Subdivide each closed contour (or hole) into vertices (pixels on the contour or the original control points).
7.1.2.
Apply DCE to each closed polygon.
Gradually remove the vertices with the smallest contribution in order to remove noise and small protrusions, without shifting the remaining vertices.
7.1.3.
Obtain a hierarchy of simplified polygons P^{n-k} (where k is the number of vertices removed).
At each step, the contour becomes coarser (with fewer vertices).
7.2.
Define the «Contour Partition».
After DCE (at the chosen level of simplification), we will obtain a set of vertices that form contour segments (arcs) on each closed contour.
For figures with holes, there will be multiple closed contours (outer and inner).
Each loop is simplified and becomes a sequence of segments.
7.3.
Remove all skeleton points whose generating points lie in the same small contour segment.
7.4.
Check «arc connectivity» to avoid breaking the topology (for figures with holes).
If the figure has inner contours (holes), there might be a case where CS(|x,y|) (Definition 2 from Article) consists of several disjoint arcs (on different boundaries).
Then it is necessary to preserve the corresponding part of the skeleton (otherwise the topology could be broken).
7.5.
After removing all unimportant skeleton points (those whose «generating points» lie in one segment), the program obtains a pruned skeleton.
Theorems 1 and 2 in Article state that the topology (the number of holes and the connectivity) is preserved if one strictly removes those skeleton branches tied to «unimportant» contour segments.
In practice, this means that one does not remove the large components of the skeleton (branches leading to significant protrusions), since their «generating points» cross several partition arcs.
7.6.
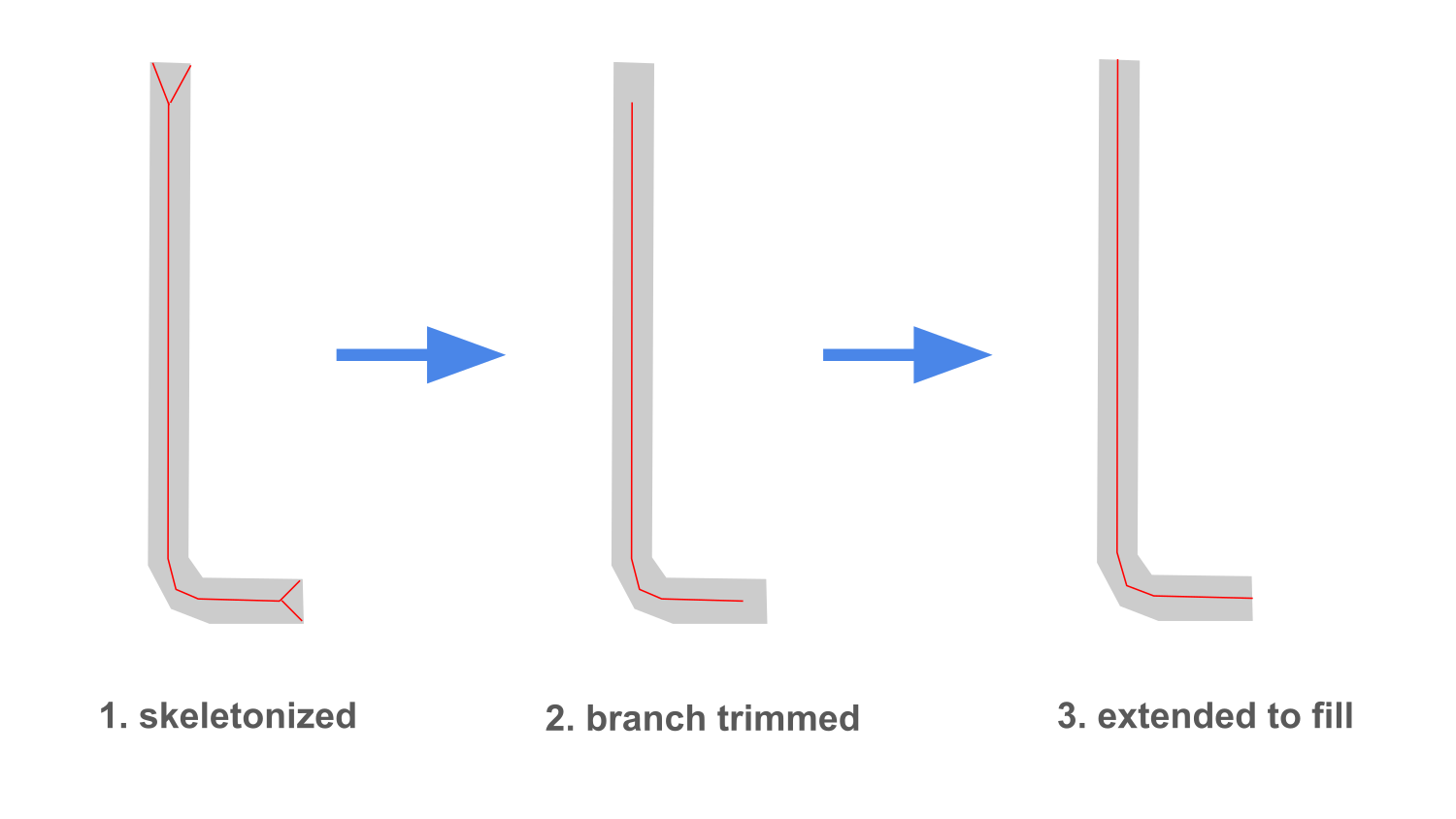
As a result, Alg yields a hierarchical skeleton in which short branches are removed while the main axes are preserved.
If needed, the steps can be repeated with a coarser DCE level to further reduce the skeleton.
8.
Extend the skeleton ends:
8.1.
Among the nodes (or pixels) of the skeleton, find endpoints — those that have degree 1.
8.2.
For each skeleton endpoint, cast a ray or a short segment outward until it reaches the nearest boundary point.